[ Reprinted from: Radio-Electronics Magazine, April 1986 ]
Abstract
Are gravitational waves the source of noise in electronic devices? The author believes so, and describes a simple circuit to detect the waves.
The author has developed a new cosmology that predicts the existence of a new type of gravitational signal. We are publishing the results of some of his experiments in the hope that it will foster experimentation as well as alternate explanations for his results.
Einstein predicted the existence of gravity waves -- the counterpart of light and radio waves -- many years ago. However, he predicted the existence of quadrature-type gravity waves. Unfortunately, no one has been able to detect quadrature-type gravity waves.
Consequently, the author developed, over the years, a new cosmology, or theory of the universe, in which monopole gravity waves are predicted. The author's theory does not preclude the existence of Einsteinian gravity waves, but they are viewed as being extremely weak, very long in wavelength, and therefore very difficult to detect unequivocally. Monopole signals, however, are relatively strong, so they are much more easily detected.
Monopole gravity waves have been detected for many years; it's just that we've been used to calling them 1/f "noise" signals or flicker noise. Those noise signals can be seen in low-frequency electronic circuits. More recently, such signals have been called Microwave Background Radiation (MBR); most scientists believe that to be a relic of the so-called "big bang" that created the universe.
In the author's cosmology, the universe is considered to be a finite, spherical, closed system; in other words, it is a black body.
Monopole gravity waves "propagate" any distance in Planck time, which is about 10-44 seconds; hence, their effects appear everywhere almost instantaneously. The sum total of background flux in the universe gives rise to the observed microwave temperature, in our universe, of about three degrees kelvin.
Sources of monopole gravity waves include common astrophysical phenomena like supernovas, novas, starquakes, etc., as well as earthly phenomena like earthquakes, core movements, etc. Those sorts of cosmic and earthly events cause delectable temporary variations in the amount of gravitational-impulse radiation present in the universe.
Novas, especially supernovas (which are large exploding stars), are very effective generators of oscillatory monopole gravity waves. Those signals have a Gaussian waveshape and a lifetime of only a few tens of milliseconds. They can readily impart a portion of their energy to free particles like molecules, atoms, and electrons.
The background flux, in general, is fairly constant. Variations in the background flux are caused by movements of large mass concentrations like galaxies, super-galaxies, and black holes.
These movements create gravitational "shadows," analogous to optical shadows. When the earth-moon-sun alignment is just right, the gravitational shadow of a small, highly concentrated mass -- a black hole, for example -- can be detected and tracked from the Earth. So, keeping those facts in mind, let's look at several practical methods of detecting gravitational energy.
Electrons and Capacitors
As stated above, gravity-wave energy can be imparted to ordinary objects. Of special interest to us are the loosely-bound electrons in ordinary capacitors. Perhaps you have wondered how a discharged high-valued electrolytic capacitor (say 1000 uF at 35 volts) can develop a charge even though it is disconnected from an electrical circuit.
While some of that charging could be attributed to a chemical reaction in the capacitor, I believe that much of it is caused by gravity-wave impulses bathing the capacitor at all times. And the means by which gravity waves transfer energy is similar to another means of energy transfer that is well known to readers of Radio-Electronics: the electric field.
As shown in Figure (1a), the presence of a large mass near the plates of a capacitor causes a polarized alignment of the molecules in the capacitor, as though an external DC voltage had been applied to the capacitor, as shown in Figure (1b).
Figure 1
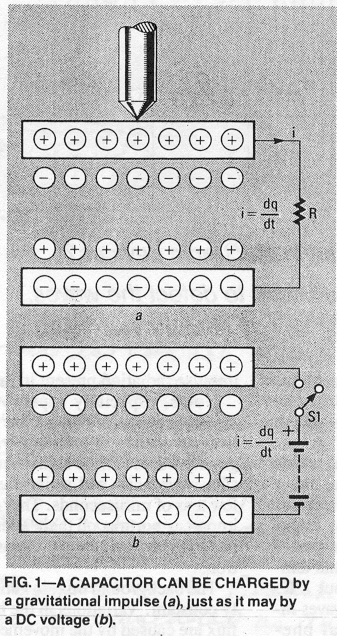
You can verify that yourself: Drop a fully-discharged 1000-uF, 35-volt electrolytic capacitor broadside on a hard surface from a height of two or three feet. Then measure the voltage across the capacitor with a high-impedance voltmeter.
You will find a voltage of about 10 to 50 mV. Drop the capacitor several times on opposite sides, don't let it bounce, and note how charge builds up to a saturation level that may be as high as one volt.
In that experiment, the energy of free-fall is converted to polarization energy in the capacitor. The loosely-bound electrons are literally "jarred" into new polarization positions.
In a similar manner, gravitational impulses from space "jar" electrons into new polarization positions.
Here's another experiment: Monitor a group of similar capacitors that have reached equilibrium conditions while being bathed by normal background gravitational impulses.
You'll observe that, over a period of time, the voltage across all those open-circuited capacitors will be equal, and that it will depend only on the average background flux at the time. Temperature should be kept constant for that experiment.
I interpret those facts to mean that a capacitor develops a charge that reflects the monopole gravity-wave signals existing at that particular location in the universe. So, although another device could be used, we will use a capacitor as the sensing element in the gravity-wave detectors described next.
The Simplest Detector
Monopole gravity waves generate small impulse currents that may be coupled to an op-amp configured as a current-to-voltage converter, as shown in Figure (2). The current-to-voltage converter is a nearly lossless current-measuring device.
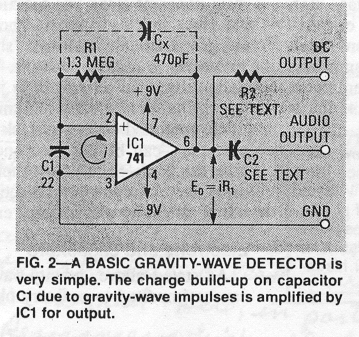
It gives an output voltage that is proportional to the product of the input current (which can be in the picoampere range) and resistor R1. Linearity is assured because the non-DC-connected capacitor maintains the op-amp's input terminals at virtual ground.
The detector's output may be coupled to a high-impedance digital or analog voltmeter, an audio amplifier, or an oscilloscope. In addition, a chart recorder could be used to record the DC output over a period of time, thus providing a record of long-term "shadow-drift" effects.
Resistor R2 and capacitor C2 protect the output of the circuit; their values will depend on what you're driving. To experiment, try a 1k resistor and a 0.1 uF capacitor.
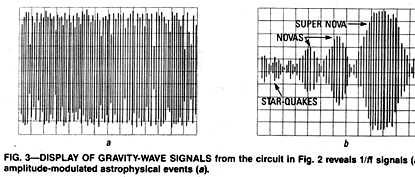
The output of the detector (Eo) may appear in two forms, depending on whether or not stabilizing capacitor Cx is connected. When it is, the output will be highly amplified 1/f noise signals, as shown in Figure (3a).
Without Cx, the circuit becomes a "ringing" circuit with a slowly decaying output that has a resonant frequency of 500-600 Hz for the component values shown. In that configuration, the circuit is a Quantum Non-Demolition (QND) circuit, as astrophysicists call it; it will now actually display the amplitude variations (waveshapes) of the passing gravitational-impulse bursts, as shown in Figure (3b).
An interesting variation on the detector may be built by increasing the value of sensing capacitor C1 to about 1000-1600 uF. After circuit stability is achieved, the circuit will respond to almost all gravity-wave signals in the universe. By listening carefully to the audio output of the detector you can hear not only normal 1/f noise, but also many "musical" sounds of space, as well as other effects that will not be disclosed here.
Figure 3
An Improved Detector
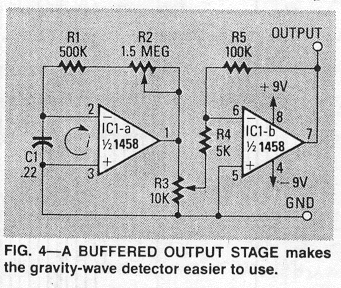
Adding a buffer stage to the basic circuit, as shown in Figure (4), makes the detector easier to work with. The IC used is a common 1458 (which is a dual 741). One op-amp is used as the detector, and the other op-amp multiplies the detector's output by a factor of 20. Potentiometer R3 is used to adjust the output to the desired level.
Figure 4
When used unshielded, the circuits presented here are not only sensitive detectors of gravitational impulses, but also of ‘electromagnetic’ signals ranging from 50-500 GHz! Hence, these circuits could be used to detect many types of signals, including radar signals.
To detect only gravity waves, and not EMI, the circuit should be shielded against all electromagnetic radiation. Both circuits are low in cost and easy to build. Assembly is non-critical, although proper wiring practices should be followed.
Initially, you should use the op-amps specified; don't experiment with other devices until you attain satisfactory results with the devices called for. Later you can experiment with other components, like low-power op-amps, especially CMOS types, which have diodes across their inputs to protect them against high input voltages.
Those diodes make them much less sensitive to electromagnetic radiation, so circuits that use those devices may be used to detect gravity-waves without shielding.
The circuit in Figure (4) is the QND or ringing type, but the feedback resistance is variable from 0.5 to 2 megohms. That allows you to tune the circuit to the natural oscillating frequency of different astrophysical events.
Huge supernova bursts, for example, have much larger amplitudes, and much lower frequencies of oscillation than normal supernovas and novas. Hence you can tune the detector for the supernova burst rate that interests you. With the component values given in Figure (4), the resonant frequency of the circuit can be varied between 300-900 Hz. The circuit of Figure (4), or a variant thereof, was used to obtain all the experimental data discussed below.
In addition, the circuits that we've described in this article were built in an aluminum chassis and then located within an additional steel box to reduce pickup of stray EMI. Power and output connections were made through filter-type feedthrough capacitors.
In the QND mode, coupling the detector's output to an audio amplifier and an oscilloscope gives impressive sound and sight effects.
Fluctuations generally reflect passing gravitational shadows. The author has taken much data of the sort to be discussed; let's examine a few samples of that data to indicate the kind of results you can expect, and ways of interpreting those results.
Sample Scans
Shown in Figure (5) is an unusual structure that was repeated exactly the next day, but four minutes earlier. The pattern was followed for several weeks, moving four minutes earlier per day.
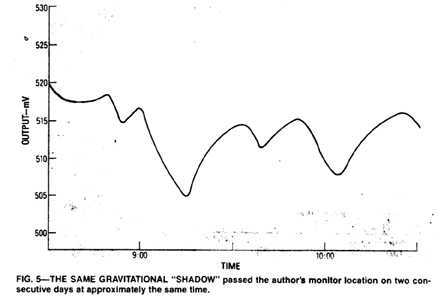
That confirms the observation that the burst response of the detector was related to our location on earth with respect to the rest of the universe. The change of four minutes per day corresponds with the relative movements of the earth and the body that was casting the "shadow."
The plot of Figure (6) appears to be a supernova, probably in our own galaxy, caught in the act of exploding. The plot of Figure (7) was made four days after another supernova explosion; that plot reveals that that supernova left a well-developed black hole and "ring" structure.
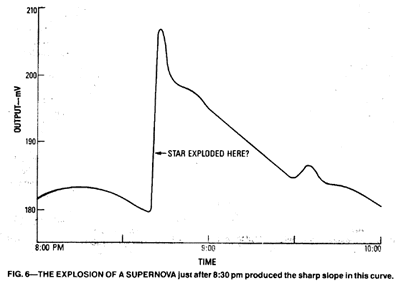
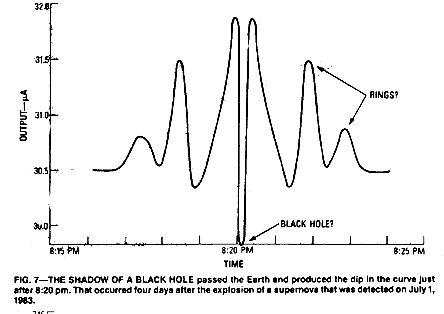
You may find it interesting to consider that visual indications of those supernovas will not be seen for several thousand years! As such, it might be "quite a while" before we get a visual confirmation of our suspected supernova!
Last, Figure (8) shows a plot of the moon's gravitational shadow during the eclipse of May 30, 1984. Note that the gravitational shadow preceded the optical shadow by about eight minutes!
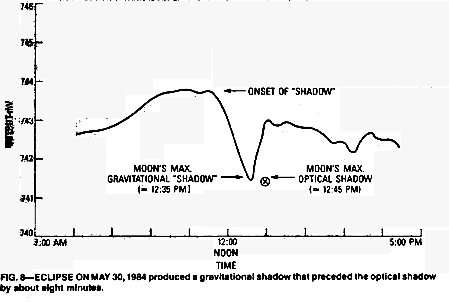
That gives credence to our claim that gravitational effects propagate instantaneously. Relatedly, but not shown here, a deep shadow is consistently detected whenever the center of the galaxy appears on the meridian (180 degrees), hinting of the existence of a "black hole" in that region.
Conclusions
In this article we discussed the highlights of a new theory of the universe that predicts the existence of monopole gravity waves. We then presented details of a circuit that can be used to detect monopole gravity waves.
The author has monitored those signals for ten years so is confident that you will be able to duplicate those results. Needless to say, the subject of gravity waves is a largely unexplored one, and there is much yet to be learned.
Perhaps this article will inspire you to contribute to that knowledge. In your experiments, you might consider trying the following: Operate several detector circuits at the same time and record the results.
Separate the detectors -- even by many miles -- and record their outputs. In such experiments, the author found that the circuits' outputs were very similar. Those results would seem to count out local EMI or pure random noise as the cause of the circuit response.
For more information on the subject of gravity you might consult Gravitation by C. Misner, K. Thorne, and J. Wheeler, published by W.H. Freeman and Co., 1973. Also, the article "Quantum Non-Demolition Measurements" in Science, Volume 209, August 1,1980 contains useful information on the QND type of measurement used here.
Sidebar: Rhysmonic Cosmology
Ancient and Renaissance physicists postulated the existence of an all-pervasive medium they called the aether. Since the advent of sub-atomic physics and relativity, theories of the aether have fallen into disuse.
Rhysmonic cosmology postulates the existence of rhysmons, which are the fundamental particles of nature, and which pervade the universe, as does the aether.
Each rhysmon has the attributes of size, shape, position, and velocity; rhysmons are arranged in space in a matrix structure, the density of which varies according to position in the universe.
The matrix structure of rhysmons in free space gives rise to the fundamental units of length, time, velocity, mass, volume, density, and energy discovered by physicist Max Planck.
Fundamental postulates of the Rhysmonic Universe can be summarized as follows:
The universe is finite and spherical Euclidean geometry is sufficient to describe Rhysmonic Space.
The edge of the universe is a perfect reflector of energy.
Matter forms only in the central portion of the universe.
The matrix structure of rhysmons allows the instantaneous transmission of energy along a straight line, called an energy vector, from the point of origin to the edge of the universe, where it would be reflected according to laws similar those governing spherical optics.
In Rhysmonic Cosmology, mass, inertia, and energy are treated as they are in classical mechanics. Mass arises, according to the author, because particles in rhysmonic cosmology must be the result of changes in the `density' of the rhysmonic structure, since the universe is nothing more than rhysmons and the void."
In a "dense" area of the universe, such as the core of a particle, a number of rhysmons are squeezed together. This means that every particle has a correlating anti-particle, or an area of correspondingly low density. In addition, a particle has an excess of outward-directed energy vectors, and an anti-particle has an excess of inward-directed energy vectors. Those vectors are what we usually call electric charge.
Gravity is not a force of attraction between objects; rather, two objects are impelled towards each other by energy vectors impinging on the surfaces of those objects that do not face each other. Newton's laws of gravitation hold, although their derivation is different than in Newton's system.
Gravitational waves arise in various ways, but, in general, a large astronomical disturbance, such as the explosion of a supernova, instantaneously modulates the rhysmonic energy vectors. That modulation might then appear, for example, superimposed on the Earth's gravitational-field flux -- and it would be detectable by circuits like those described here.
Parts List - Simple Detector
R1 - 1.3 megohm, 1/4 watt, 5%
R2 - see text; 1/4 watt. 5%
C1 - 0.22 uF
C2 - see text
Cx - see text
IC1 - 741 op-amp
IC1 - 1458 dual op-amp
Parts List - Buffered Detector
All fixed resistors 1/4-watt, 5%.
R1 - 500,000 ohms, 1/4-watt, 5%.
R2 - 1.5 megohms, potentiometer, 1/4-watt, 5%.
R3 - 10,000 ohms, potentiometer, 1/4-watt, 5%.
R4 - 5000 ohms, 1/4-watt, 5%.
R5 - 100,000 ohms, 1/4-watt, 5%.
C1 - 0.22 uF