Simple Electronic Gravity Meters Display Interesting Gravity Effects

 

Abstract

Astrophysicists have been attempting to detect the elusive quadrupole-type gravity signals predicted by Einstein without unequivocal success so far. However, Newtonian-type gravitational force field gradients have actually been detected for many years now as noise in electronic devices. The simple electronic-type of gravimeter described here greatly amplifies electronic noise and resolves it into meaningful displays on an analog meter or a strip recorder unit. The inquisitive and interested electronic experimenter can thus enter at a low cost into an exciting exploration of our universe in terms of these gravity signals, especially if a strip chart recorder unit or a computer unit is used to store and display the tremendous amount of information present in these data. The author hopes that many will opt to do so.

 

Background

Gravimeters (or gravity meters) are used to measure the relative strength of a gravitational force field at some particular location for a number of reasons. One very common reason is to determine the possible presence of large underground mass anomalies which, in turn, could signify the presence of potential mineral, oil, or gas deposits. The commercial gravimeters used in many of these evaluations are generally both very expensive and also very delicate. However, the electronic experimenter may construct a very simple low-cost electronic-type gravimeter which is highly portable, rugged, and yet extremely sensitive to even minor variations in the earth’s g-field. Therefore, it will not only indicate variations in gravity due to local mass variations, but it will also respond to the many fluctuations in the earth’s gravity field which are due to cosmic-generated gradients and even the presence of astronomically-distant very dense masses which may happen to lie on the instantaneous astronomical meridian position of the gravimeter. The meridian position as defined here is essentially the same as the geographical longitude of the location of the gravimeter unit.

Newtonian gravitational force field gradients, i.e., scalar field type gradients, have been noted by the author for many years now (Ref. 1). Simple detectors of the electronic type (Ref. 2) and the spring scale type (Ref. 3) have been used in these detections. The electronic version to be considered here is extremely simple, requiring but a few readily available electronic components which may be easily assembled by the average electronic experimenter or amateur scientist. It should be of special interest to amateur astronomers engaged in either optical or radio astronomy as well as to many professional astrophysicists.

 

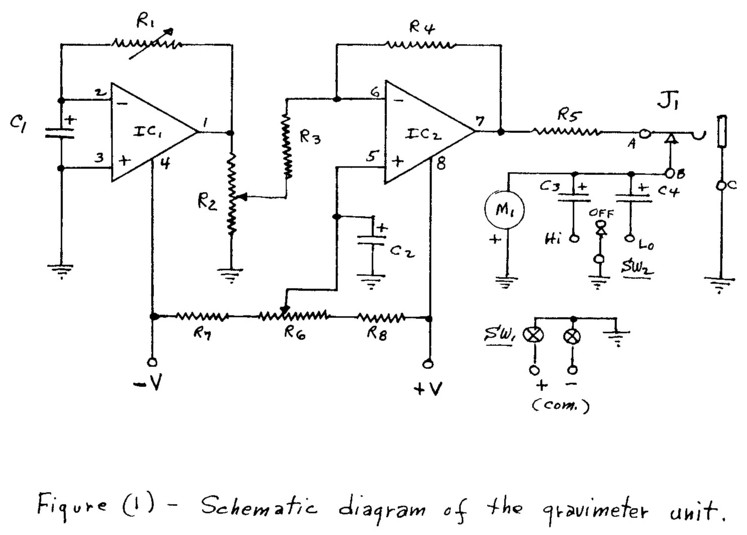
Figure 1 ---Schematic diagram of the gravimeter unit

 

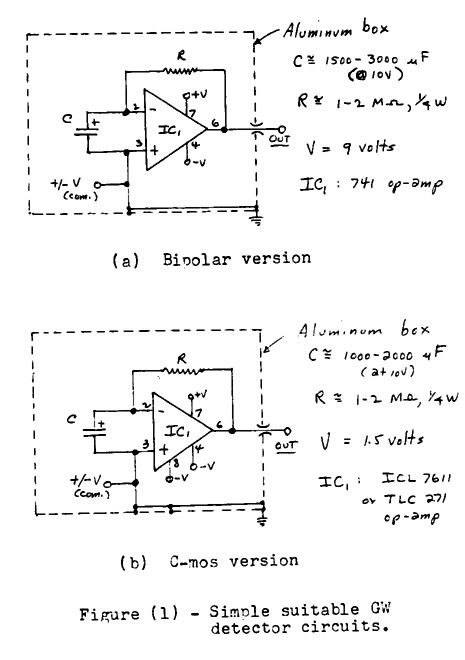
How it Works

The circuit for these particular demonstration units is given in Figure 1. One version uses a single low-cost C-MOS type operational amplifier device (a dual section unit) which can work well with but a low level 1.5 volt battery supply. The low current drain of these op-amps should enable long life fro the small alkaline AAA cells used to internally power this unit. The second version is similar in design but uses the ore generally available low-cost bipolar-type of op-amp devices. The operation of the C-MOS unit will be described in detail here. However, the bipolar unit, while quite similar, requires some component value changes as well as a higher power supply voltage. These changes are noted in the Parts List for these units.

In the C-MOS version, Newtonian gravitational force field gradients interact with the electron-ion structure of the dielectric in the 1000 uF input capacitor C₁, to generate small current fluctuations from that capacitor and these fluctuations will reflect the gravity gradients being intercepts by that capacitor. Section IC₁ of the op-amp is operated in the current-to-voltage conversion mode and the small input current fluctuations from capacitor C₁ are converted to much higher voltage fluctuations. The sensitivity of this stage is controllable by the high resistance feedback resistor, R₁. Output from the detector section IC₁ is then coupled out through a gain control potentiometer, R₂, to drive a conventional inverting amplifier, IC₂, which has about a x20 voltage gain. An offset control, R₆, in the non-inverting input of IC₂ is used to establish the operating position of the averaged gravity-induced output levels on the analog display meter, M₁. the display meter is a 100 uA meter operated as a 0-1 volt voltmeter in conjunction with the series resistor, R₅. Capacitors C₃ and C₄ form part of a low-pass filter network (utilizing R₅ also) to establish a time constant for integration of the meter response to the gravity fluctuation signals. A very long time constant, i.e., a very low cut-off frequency for the LP filter, is used to largely measure the averaged gravity levels, while the shorter time constants are used to monitor the more rapidly varying responses of the ore distant astronomical events. The switch SW₂ provides for three levels of integration. A DPST switch, SW₁, is used to interrupt the common return leads of the dual power supply used separately while in the off position. This is necessary to avoid the small battery drain that would occur is a SPST switch were used here. The output jack, J₁, provides for an output to any external device such as an external meter, an audio amplifier, a strip chart recorder, or a computer unit, if desired. To avoid possible RFI problems, the unit should be fabricated in a Faraday type shielded enclosure. A simple aluminum box enclosure containing the entire circuitry, including the battery supply, should be adequate for most observing locations.

 

Testing The Unit

After the electronic experimenter has checked out his circuit components and the circuit wiring, the 1.5 volt batteries may be inserted into their holders. Keep the power switch, SW₁, off at this time. Turn the sensitivity (feedback) control, R₁, to its mid-position, the gain control, R₂, to its minimum position, the offset control, R6 to its mid-position, and the integration switch, SW₂, to the off position. Now turn on the power switch and if the unit is operating properly a meter deflection near center scale should be noted. Center the pointer with the off-set control, R6. The off-set control is very sensitive and should adjusted carefully. Now slowly increase the gain control about one-quarter turn. If no indications are seen on the display meter, or if the meter foes of scale, the input capacitor may have an excess residual charge on it. This charge should leak off in a minute or so but may be discharged more rapidly by turning down the sensitivity control to its shorted position momentarily, and then returning it to the mid-position again. Since the integration switch, SW₂, had been set to its fastest response time, rapid fluctuations should now be seen on the analog meter output, that is if good components were used and the circuit wiring was correct. The fluctuations may now be better centered on the display meter with the off-set control and their amplitudes adjusted to suitable levels with the gain control. Do not increase the gain to the point of overdrive or to the point where there will be a tendency to low frequency oscillations which will be sustained by occasional high level fluctuations from the cosmos. Notice the varied and wide amplitude ranges of the display!

With the integration switch in its off position, the unit largely responds to the rapid fluctuations due to distant cosmic events. With the switch in the Lo position, it will respond mainly to colder-by cosmic events and this position may also be used to determine the averaged gravity field levels, especially if even a longer integration time is used, e.g., the output shunt capacitance is increased more. When the integration switch is in the Hi position, the unit will respond to many interesting cosmic events in our own Galaxy region as well as the Local Group of galaxies. The reason for this type of response is that the resolution of the detector ‘beam’ is extremely fine, since the aperture for this detection system is essentially the active area of capacitor C₁, and that may be only in the order of 1/4 to 1/2 inch in diameter. Thus this fine beam sweeps the meridian position of the detector as a function of the rotation of the earth. Simple geometry shows that such a fine beam would sweep across some distant object more rapidly than it would do so for some similar but much nearer object. Thus the difference in response times.

 

Typical Responses

Since these fluctuations are a function of time, they are best displayed on a strip chart recorder unit running at about a chart speed of 2 to 4 inches per minute. A high input impedance strip chart reorder unit must be used with the C-MOS deice detector unit, but a low impedance strip chart recorder unit could be used with the bipolar detector unit, e.g., a D’Arsonval meter type unit. In both cases, the output voltage could range between 0 volts and about 1.5 volts. Some typical responses as seen on a strip chart recorder are shown in Figure 2. Experimenters who lack a strip recorder or a computer unit ay try to follow some of the slower responses by hand recording the output data being received when the unit is operated with very long output integration times. Even here, the experimenter can expect to observe some local cosmic events of the type shown in Figure 2. However, recording the data by hand can be quite tedious and very difficult at best.

 

Figure 2 --- Some recorded gravity signals

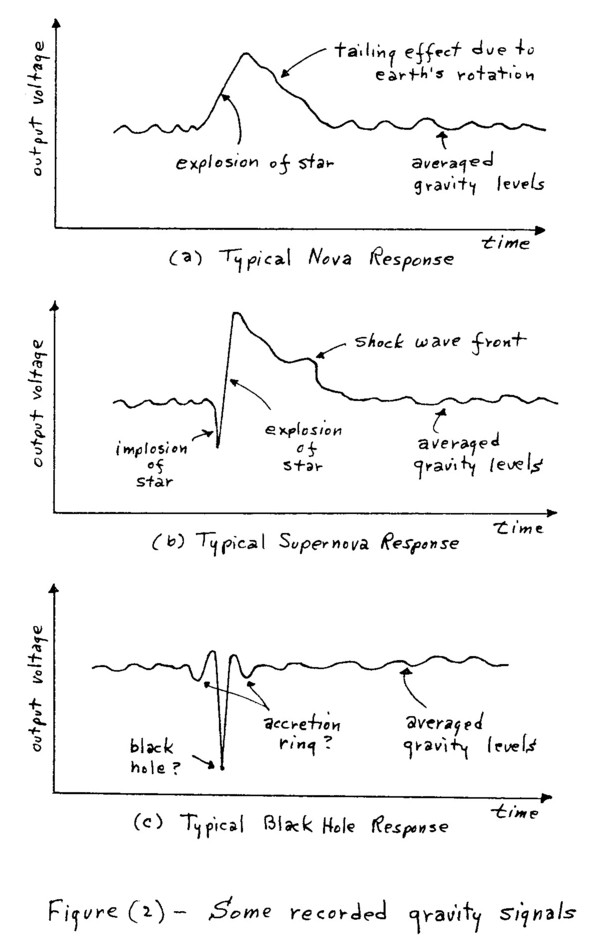
Briefly stated, some of the cosmic events detectable with these units are cosmic events which were predicted by the astrophysicists but not yet detected by them, primarily because most of these astrophysicists are still looking for the elusive quadrupole-type gravity signals which were predicted by Einstein. However, these units detect the longitudinal gravitational force field gradients of the Newtonian type (which were no supposed to exist, incorrectly so, in terms of the presently prevailing relativity theories!). Therefore, the interested electronic experimenters, amateur scientists, as well as the professional researchers, now have a golden opportunity to enter into a low-cost exploration of our universe using the proven techniques disclosed here.

Many of the active astronomical events detectable with these units appear to be nova and supernovae. Novae are believed to be stars which lose much of their outer layers in a nuclear-type explosion. These events are detectable (and quite often) since the rapid expansion of the star’s outer mass causes a Newtonian force field gradient, which, if it happens to lie on the detector’s meridian position, causes a superposition of fields on the earth’s gravity field, and thus results in a measurable change in the earth’s gravity field. Supernovae are believed to be large stars which implode to a neutron star or black hole type of structure, and then blasts of much of their volume and atmosphere. The response as detected by these units shows both the implosion and the explosion of the event. After a massive supernova event, the neutron star or black hole type of structure, i.e., a very small very dense mass, is generally seen at that location, often accompanied by what the astrophysicists have termed an accretion ring. The units also detect what appear to be very dense masses but without an accretion ring. These may be very old black holes which have since lost their accretion rings.

 

The Bipolar Detection Unit

The bipolar device detection unit is very similar to the C-mos device unit described above, but requires some component value changes as well as the power supply change as shown in the Parts Lists. These changes were made in order to essentially duplicate the responses as seen wit the C-mos device unit. The bipolar device unit works well with an internal 9-volt battery supply. Most experimenters may prefer to use the bipolar device op-amps since they are generally available. The author uses the bipolar device design to drive his D’Arsonval meter type strip recorder unit.

The experimenter is cautioned here that while the basic design of these detectors is very simple, components and devices do vary. The experimenter may wish to try several electrolytic capacitors or op-amp devices if difficulty is seen in achieving the effect given here. Especially the bipolar op-amp devices, even if they are labeled the same, may be quite different in structure and performance; some might even have different pin-outs. The author has constructed many detector units (and many colleagues also have done so) so that he has confidence that the careful and patient researcher, amateur and professional, will be able to duplicate these results.

 

Conclusions

The simple low-cost electronic type gravity meters described here should enable the electronic experimenter not only to determine the averaged gravity forces at various locations, but also enter into the fascinating and quite unexplored area of gravitational field astronomy. Outside of possibly obtaining a strip chart recorder as a highly desirable component for use in these studies, the experimenter is not otherwise limited by extensive or expensive facilities or preferred locations in pursuing these objective. Many experimenters, mainly amateur radio operators (hams) have entered the area of radio astronomy successfully. However, compared to the above disclosed gravity field astronomy, radio astronomy is rather expensive, tricky, and involves fairly massive antennas as well as requiring fairly radio-quiet, i.e., EMI-free locations. Gravity signal astronomy can be done at any location, even electrically noisy locations, provided the units are adequately Faraday shielded. Simple aluminum box enclosures are adequate for most locations. The author does his observing in a corner of his basemen lab area. The author hopes that many experimenters, both amateur and professional, will opt to enter into these investigations. Good luck with your experiments!

 

References

(1) Gregory Hodowanec: Background on the Possible Bevelopment of a Simple Gravity Wave Detector (June 1980).

(2) G. Hodowanec: Gravitational Waves?; Radio-Electronics (April 1986).

(3) G. Hodowanec: Simple Gravimeer Dtects Gravity Shadow Signals; Tesla ’86 (March-April 1986).

 

Added Notes

(1) Place a 0.01 uF ceramic capacitor across output jack J₁, terminal A and C for improved RFI isolation, if necessary.

(2) The low impedance output of the op-amp should normally be loaded with a low impedance meter or strip chart recorder unit. However, if a high-impedance meter or a potentiometric-type strip chart recorder is used, it may be necessary to load the output with a 1-2 K Ohm resistance and use the voltage drop across this resistance as the output signal. All loads should be resistive. Reactive loads could present scalar-type signal feedback to the detector and result in instabilities.

 

Parts Lists

For the C-mos device unit:

R₁ --- 5 megohm, miniature potentiometer
R₂ --- 10,000 ohms, miniature potentiometer
R₃ --- 4,700 ohms, 1/4 watt, 5%, resistor
R₄ --- 100,000 ohms, 1/4 watt, 5%, resistor
R₅ --- 10,000 ohms, 1/4 watt, 5%, resistor
R₆ --- 25,000 ohms, miniature potentiometer
R₇, R₈ --- 50,000 ohms, 1/4 watt, 5%, resistor
C₁ --- 1000 uF, 10 V, electrolytic capacitor
C₂ --- 10 uF, 10 V, ohms, electrolytic capacitor
C₃ --- 470 uF, 10 V, electrolytic capacitor
C₄ --- 2,200 uF, 10 V, electrolytic capacitor
SW₁ --- DPST, miniature switch
SW₂ --- SPDT (center off), miniature switch
J₁ --- miniature closed circuit jack
IC₁, IC₂ --- Dual op-amp (C-mos): ICL7621 (ok), TLC272 (used)
M₁ --- 100 uA meter (0-1 scale)
V --- 1.5 volt battery

For the bipolar device unit:

R₄ --- 470,000 ohms, 1/4 watt, 5%, resistor
R₅ --- 1,000 ohms, 1/4 watt, 5%, resistor
R₇, R₈ --- 100,000 ohms, 1/4 watt, 5%, resistor
C₁ --- 2,200 uF, 10 V, electrolytic capacitor
IC₁, IC₂ --- Dual operational amplifier (bipolar); 1458 (used)
M₁ --- 1 mA meter (0-1 scale)
V --- 9-volt battery

Note: The other components are the same as above.