Simple Gravimeters for the Amateur Scientists
Abstract:
Gravimeters (gravity meters) are devices which measure the averaged acceleration of the earth’s gravity field. Such instrumentation is best known for its use in determining changes in the earth’s gravity field which may be due to variations in buried masses in the earth. Such mass density variations could indicate the presence of oil or mineral deposits and thus gravimeters are used in prospecting. Most such gravimeters are but specialized sensitive scale systems in which the position of a fixed mass as a function of gravity field variations can be suitably recorded. However, in order to minimize spurious responses due to local vibrations, temperature changes, winds, etc., complicated suspension methods are employed making such instruments much too costly for the average electronic experimenter-scientist. Described here, however, are a number of simple gravimeters, both mechanical and electronic in design, which can easily be built by the average electronic experimenter. While the units are sensitive enough for prospecting purposes, the amateur scientist may be more interested in observing gravity variations which are believed to be due to extraterrestrial gravitational effects. A number of repeatable variations are described and possible sources for these variations are given. Moreover, a number of other applications for the gravimeter are also described which should interest the experimenter. It is hoped that this material will foster increased interest in gravity and gravitation by the young experimenter-scientist who will be the foundation of our future scientific community.
Introduction:
Gravitation, per se, is a well-known force which is experienced by all people. Many see it in the actions of falling bodies, but especially notice its effect on their very own bodies as their weight. The force is unique in that while it is a matter of common everyday experience, it yet remains quite an enigma with respect to its true nature. Many also realize that the force of gravity is related to an object’s mass, e.g., if one has more body mass, one is ‘heavier’, and that such ‘heaviness’ can be measured by scale systems. But how such gravity fields interact with mass remains very much a mystery to mankind even though many theories have been advanced to explain that effect. Foremost among these have been the relations as developed by Newton and Einstein, but those relations really only ‘describe the effect’ and do not explain the true nature of gravitation. Yet such explanations are useful in providing a basis for a study of the earth’s gravity field.
Gravity Defined:
The effect where bodies apparently ‘attract’ each other is quantitatively summed up in the law of Universal gravitation as developed by Newton. Here, the force of attraction between two bodies, m, M, separated by a distance r is given by:
F = Gm M / r2,
Where G is the so-called gravitational constant and has a value of about 6.67 x 10-8 if the centimeter-gram-second (CGS)system of units are used. The gravitational field at any point is given by the force exerted on a unit mass at that point. The field intensity at a distance r from a point mass m is thus Gm/r2 and acts toward m. The gravitational potential V at that point is the work done in moving a unit mass from infinity to that point against the field. Therefore,
V = -Gm/r
And it is a scalar quantity measured in ergs per gram when the CGS units are used. While Newtonian gravity is describable as an ‘attraction’ between two masses as depicted in Figure (1a), Einstein gravity is visualized as a curvature or warping of space and time around a massive body and us usually depicted as shown in Figure (1b). However, here we will be more concerned with the earth’s gravity field as defined by the ‘weight’ of an object.
Figure (1): Simplified present-day views on the phenomenon of gravitation ~
(1a) Newtonian Gravitation: F = Gmm / r2 . For example, when the masses m are one gram each, and the spacing between the mass centers is one centimeter, then the force of attraction F is equal to:
6.67 x 10-8 dynes.
(1b):Einstein Gravitation: (top) Curved path of a small particle around a larer mass due to the warping of space-time in the region around this more massive particle, M.; (bottom) Path of a small particle in space-time in the absence of the more massive particle, M.
Weight Defined:
In its simplest terms, weight is generally defined as the force with which a test body is attracted toward the center of the earth. In terms of Newton’s Law this becomes:
Force = Weight = W = mMG / R2 ,
Where m is the test mass, M is the mass of the earth, R is the radius of the earth, and G is the gravitational constant. This weight will be in poundals (using English units) and in dynes (using metric units). The above equation may be simplified to:
W = mg , where g = MG / R2 .
The value of g is a measure of the acceleration of the earth’s gravity field (free fall) near the earth’s surface and is generally considered to be constant at a particular location on earth. Thus this relation is similar to the familiar F = ma seen in mechanics. The value of g is in the order of 32 ft/sec2 or 980 cm/sec2. Since weight depends upon the amount of mass and the acceleration of gravity, a definition of a standard weight would require the fixation of this mass amount and also a location on earth where this weight was determined. By international convention, the standard mass is the International Prototype Kilogramme and is represented by a platinum-iridium standard preserved near Paris, France. Other secondary standards, based upon this primary standard, are located in other countries as well.
Dependency of Weight on Geographical Location:
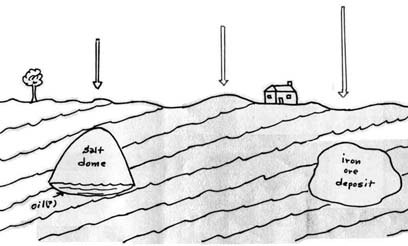
It can be seen from the above equations that weight on earth is dependent on the earth mass, M, the earth radius, R, and the gravitational constant, G. The earth mass may be assumed constant and if the gravitational constant is assumed constant, then the earth radius is the only variable. Its value depends upon one’s latitude position and height with respect to the surface of the earth. The radius of the earth is about 15 miles less at the poles than at the equator. In addition, centrifugal forces due to the earth’s rotation can reduce the ‘pull’ of gravity, being greatest at the equator and zero at the poles. Therefore, when consideration is taken of these factors, a ton weight (2000 lbs) that is first measured at sea-level at the north pole will be found to weigh about 7 lbs less at sea-level at the equator. Also, for example, the value of g at Paris, France, is about 32.184 ft/sec2, while the value of g at New Orleans USA would be about 32.129 ft/sec2, or about 0.17% less. While the overall mass of the earth is assumed to be constant, there may be localized variations in earth density which can and do affect the value of g locally and thus the weight. For example, the presence of a salt dome (which can signify oil deposits) may reduce the value of g above such a deposit, while ‘heavy ore’ deposits may significantly increase the value of g as depicted in Figure (2). Also, it will be shown later that the gravitational constant, G, may not really be constant in that it can be affected by certain ‘cosmological events’, both as very short term effects as well as somewhat longer term effects. Thus the accelerating factor, g, may vary at any particular location, and such variations may actually be measurable with devices which can be termed gravity meters or gravimeters.
Figure (2): Variations in g-factor due to some localized 'buried' masses.
Left: decreased g-factor; Center: nominal g-factor; Right: increaed g-factor
Mechanical Gravimeters:
Gravity meters, presently, fall into two general classes of devices of a mechanical nature, but the author will later describe gravimeter devices which are of an electronic nature. Present day mechanical gravimeters are mostly either of the pendulum type or the sensitive balance scale type.
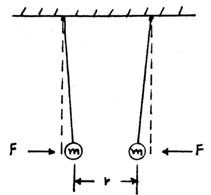
Pendulum Gravimeters: These systems have been used to obtain the most accurate determinations of the value of g at a particular location. It is shown in its most simple form in Figure (3a). Here, a small bob (weight) is suspended from a point by a light thread. The period of oscillation for small amplitude swings is determined by the formula T = 2 pi x square root of l/g, where l is the length of the thread and g is the acceleration of free fall. Thus g is simply determined here for any particular location. The most accurate measurements are made with specially protected torsion-type pendulums, such as was used in the many Cavendish type experiments in the past.
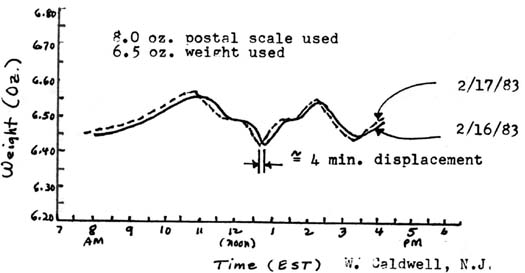
Balance Scale Gravimeters: These are, in effect, simply very sensitive spring balances in which the change in weight of a fixed mass is measured. It is shown in its simplest form in Figure (3b). A somewhat practical form of this type of gravimeter is provided by a well-made postal scale which reads but a maximum of 8 ounces. Such a scale should be able to read to the nearest 0.01 ounce. That such a scale is a valid gravimeter is seen in Figure (3c) where the unit responded to a major cosmic mass structure which always appears in the Leo region of the celestial sphere. Note the diurnal repeatability as seen with this simple device. More on this later. Some digital type scales (based on Hooke’s Law, e.g., springs) may also serve as simple gravimeters.
Figure (3a): Basic Pendulum-type Gravimeter ~
T = 2 pi x square root of l/g, from which, g = 4 pi squared x l /T2
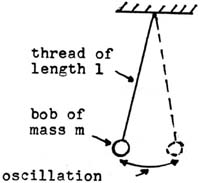
Figure (3b): Basic Spring Scale Gravimeter ~
W = mg, then if m is kept constant, and the spring obeys Hooke's Law, then: g a W.
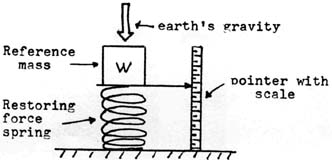
Figure (3c): Response seen with Postal Scale Gravimeter ~
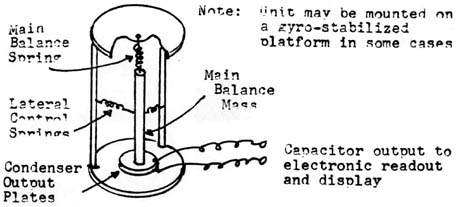
Practical mechanical gravimeters should respond only to the actual vertical variations in the value of g. Commercial gravimeters of this type are constructed so as to not only limit lateral movements due to winds, temperature variations, vibrations, etc., but also to provide for an electrical-type readout rather than a purely mechanical readout so that the variations could be electrically scored and/or displayed on some recorder unit. Therefore, these types of gravimeters are generally quite complicated and expensive, and thus beyond the means of the average amateur scientist. A depiction of a possible unit of this type is given in Figure (4a).
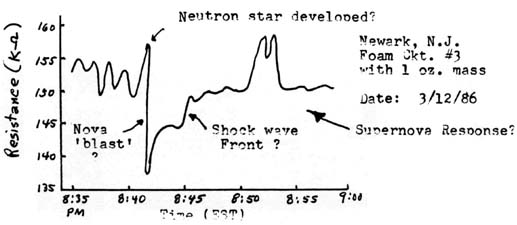
A more practical mechanical gravimeter for the amateur scientist is shown in simplest form in Figure (4b). This is a typical spring balance system, but the ‘spring’ of this system is a conductive compressible foam material, such as that which is used to safely ship very static-sensitive integrated circuits. Here, any variations in weight will appear as variation in compression of the foam and thus as variations in the resistivity of the material. The resistance can be directly measured with an ohmmeter, preferably one of the digital type. That such a device is a viable gravimeter for the amateur scientist is seen in Figure (4c) where the response of the unit to what may have been a super-nova type event in the celestial sphere was recorded. More on this later. The experimenter may wish to try different sizes of foam as well as reference weights for different sensitivity to gravity events. The amateur scientist is also cautioned to remain within the elastic limits of the foam material.
Figure (4a): Possible Commercial Gravimeter ~
Figure (4b): Novel Scale-type Gravimeter ~
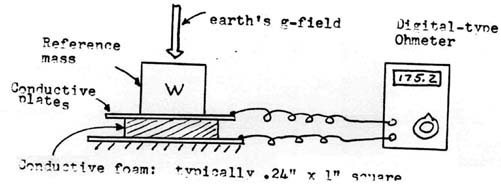
Figure (4c): Typical Response with above Gravimeter ~
Electronic Gravimeters: Over the past 15 years or so, the author has also developed many electronic-type gravimeters. Besides simplicity, the units have the advantage of ruggedness and freedom from many external influences such as vibrations, temperature effects, and electrical disturbances, and respond only to pure gravitational effects. Typical units have been described in some other publications in the past, but one of the basic low-cost units will be described here.
Practical Electronic Gravimeter: The circuit shown in Figure (5a) is extremely simple but it contains the three elements of the electronic gravity meters as developed by the author. These are (1), a detector section, (2), a low-pass filter section, and (3), the output meter. The detector section has been designed around a readily available low cost programmable operational amplifier, the TLC271 device. The unit operates at about 1 mA of current from a single 9-volt self-contained battery supply. This op-amp has extremely high input impedance and low output bias and off-set currents. It is operated with the non-inverting input off-set to approximately the midpoint of the battery supply, primarily to enable the output voltage to remain near the center of the 0-10 volt output meter scale. Some limited positioning of this operating point is provided by the calibration control, R3, so as to set a reference point for any series of measurements. Such off-set operation also enables the unit to respond to AC variations in the g-factor as well as the averaged DC component. The AC component is due to certain cosmic gravity impulses while the DC component largely reflects the relatively steady flux due to the earth’s gravity. Therefore, the detector output is passed through a very low cut-off low-pass filter to smooth out (filter or integrate) these AC variations and thus this unit is truly a gravity meter or gravimeter.
The detector section (IC1) is operated as a current-to-voltage converter device of very high gain due to the use of a very large feedback resistance, RF. The Newtonian-type gravity impulses which are superimposed upon the earth’s averaged gravity field will develop small currents from the 400 uF electrolytic input capacitor, C1, due to a gravity induced ‘polarization process’ in the dielectric material of the capacitor. The more rapid current variations may be due to such factors as cosmic novae and supernovae, but the longer term variations are largely caused by the presence of large density variations in certain masses which may be in line with the detector capacitor and the earth’s gravity field. In other words, when such dense masses are located on the detector’s meridian position (i.e., the great circle on the celestial sphere which runs on a north-south line through the zenith), the density variations are superimposed upon the earth’s gravity flux and thus are detectable with this device as changes in the DC output levels. Density variations of nearby masses are detectable as well as extremely dense remote masses such as astronomically distant ‘black hole’ structures. Thus this electronic-type gravimeter has extreme sensitivity without the problems of most mechanical type units.
For use as a g-factor measuring device (which is the role which we are considering here), the output of the unit is heavily filtered by the low pass filter made up of resistor, R4, and capacitor, C2. Capacitor C2 used here is a small 0.1 farad unit which was primarily intended for use as a keep-alive voltage unit for short term power supply failures for Cmos devices in computer units. It is available from radio Shack. Thus this gravimeter will respond only to the very slowly changing variations in the earth’s gravity field. To summarize: Capacitor, C1, is an almost ideal current generator (excited by the earth’s gravity flux) which is coupled to an operational amplifier configured as a current-to-voltage converter. This is an almost lossless current measuring scheme where the output voltage is proportional to the product of the input current and the feedback resistance. Thus the output voltage can be reasonably high even with the very low picoampere currents developed by gravity flux in the input capacitor detection element. Linearity is assured as the open circuit of the capacitor maintains the input terminal voltages to the op-amp near virtual ground, but slightly current biased by the gravity-induced polarization. The output voltage is read on the built-in voltmeter, but may also be couple out to an external meter or a recording device such as a computer or strip chart recorder by means of jack, J1.
Although the current drain for the unit is low, an on-off switch is provided to conserve battery power during non-use periods. It must be remembered that due to the long time constant of the output filter, the unit must be allowed several minutes to stabilize after turn-on. While the unit is best constructed within a metal enclosure to avoid possible RF interference (RFI), the author found that the presence of the input protective networks within the op-amp device tended to suppress such RFI responses. Thus the prototype unit was constructed in a plastic box and no RFI problems were experienced.
Figure (5a): Schematic of Simple Electronic Gravimeter ~
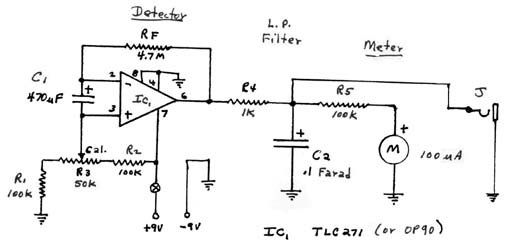
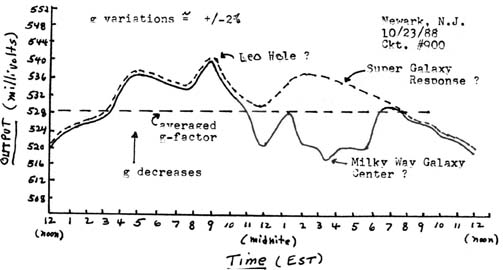
Figure (5b): Typical diurnal variation of the earth's gravity flux as measured with an electronic gravimeter ~
Electronic Gravimeter Performance:
While good performance as gravimeters may be obtainable from properly constructed and operated mechanical-type devices, the sensitivity of such units to external effects such as local vibrations or other movements generally limits their use to the amateur scientists lab area unless proper safeguards are used. The electronic gravimeter, however, does not suffer from any of these limitations and can be used anywhere, especially if a god grade of well-damped output meter is used. For a somewhat faster response to some gravity level variations, the amateur may want to reduce the value of the output filter capacitor. Perhaps a second 0.1 farad capacitor could be connected across one of the capacitors to short it out if the longer time constant filter is desired. In this way, two levels of output integration will be available, e.g., with 0.1 farad in the filter circuit, or with 0.05 farad in the filter circuit.
Therefore, it is recommended that the amateur scientist who wishes to enter this fascinating study of the earth's gravity field, begin by constructing the electronic gravimeter shown in Figure (5a). A typical diurnal variation in the measured g-factor is shown in Figure (5b). This particular gravimeter had an extra stage of DC amplification in order to better emphasize the DC variations on a strip chart recorder unit. As can be seen here, the earth's gravity flux varied about +/- 2% over a 24 hour period. These variations have been noted on all gravimeters built by the author (including mechanical-type units) and have been related by the author to the masses represented by two very large structures in our universe. One is the Milky Way Galaxy, our home galaxy, which is also optically visible to the unaided eye. The other structure, which was originally but a conjecture in the mind of the author, has since been consistently confirmed by several gravimeters. This is apparently a gigantic Super Galaxy System which forms the main body of our universe. It appears to have a spiral structure quite similar to the Milky Way galaxy. As the earth rotates on its axis, the response of the detector varies as the unit 'scans' a different meridian with this rotation. The scanning ‘beam’ size here is essentially equal to the volume of the active portion of the dielectric in the detection capacitor element, C1. Thus the gravimeter has extreme resolution. The presence of dense masses in line with the detector-meridian position will ‘modulate’ the g-factor levels, very much like translucent or opaque objects can also modulate the transmission of light beams in its path. A gravimeter using a heavily filtered (integrated) output is thus able to follow the slow changes in earth gravity levels due to ‘shadows’ introduced by our own Galaxy masses (due to its close proximity), and also the slow changes caused by the Super Galaxy masses (due to its over-riding concentration of masses). If the variation due to our Galaxy is made much more apparent as shown by the dotted line response in Figure (5b).
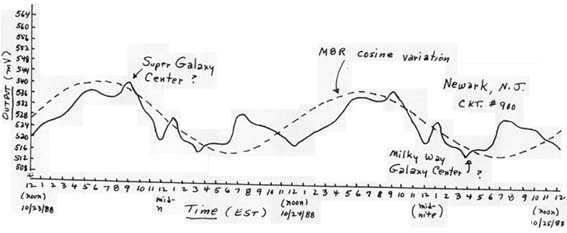
Since the dense structures in the universe are ‘seen’ on a daily basis, the response shown in Figure (5b) is shown extended for a 48 hour period in Figure 6. Plotted in this way, the response illustrates very well a cosine-type variation which also correlates very well with a cosine-type variation in the microwave background radiation levels which have been determined by a number of experimental astrophysicists in the past. These evaluations strongly suggest that the so-called microwave background radiation is but the heating manifestation of the gravitational impulse background in the universe and thus the two are one and the same. Thus this may be an alternate explanation of the background radiation rather than the so-called Big Bang theory.
Figure (6): Possible correlation between the g-factor variation and the cosine variation noted in the Microwave Background Radiation (MBR) ~
Applications of Gravimeters:
The experimenter or amateur scientist may by now be asking the question: but of what use are these gravimeters? The answer to that is that there are a great many applications once the amateur has gotten a firm understanding of the earth’s gravity and how it is affected. One very common application has already been mentioned. That is its use in mineral and oil exploration, i.e., prospecting. Generally, very expensive mechanical-type gravimeters are used by the professionals here, but the amateur prospector should be able to use this electronic gravimeter effectively in such an application. It has sufficient sensitivity to respond to earth gravity changes introduced by bending one’s own body over the unit! Allowing for the long time constant for the unit, a reduction in g-factor in the order of 1% can be observed! Based on this observation, it should be possible for a submerged submarine to determine the presence of a surface vessel directly above it by purely passive methods, and thus of some use in the military.
Another possible use for the gravimeter device, especially the more sensitive and faster responding units, are as a navigation aid device. For there are fixed dense masses in the universe, such as the Galaxy Centers shown in Figure (5b), and many, many others, which will appear on the gravimeter’s meridian position on a daily basis. Thus, the longitudinal position of a submerged submarine can be determined by this gravitational method. The celestial sphere does not have to be observed visually, and the depth of the sea waters has no effect on this response.
Another very important effect is that the gravity levels on earth may have a direct effect on the upper stratosphere jet stream patterns and thus could affect our weather patterns. As shown in Figure (5b), the gravity flux variations are now about +/- 2% daily. Prior to about December 5, 1986, the gravity flux variations were only about +/- 1%! Gravity flux changes due to a Milky Way Galaxy Center ‘event’ noted December 6, 1986 (where a possible supernova-type event had generated a new very deep ‘black hole’ (?) and accretion ring structure there) and a possible new Super Galaxy Center ‘event’ on march 14, 1988 (which also appeared to increase the depth of the ‘black hole’ there), may have been responsible for the increase in variations from 1% to 2%. These increased variations in the levels of the earth’s gravity are believed to be (in part) responsible for much of the most unusual weather conditions seen world-wide in recent months and years, as well as an increased potential for earthquakes in unstable regions of the earth.
Another use for such gravimeters has been in the detection of the many supernova events occurring in this universe. Such events are best detected with reduced filtering in the output of the detector units. Presently, the author is concerned with the possible demise of the star Betelgeuse in the constellation of Orion. The Galaxy Center event of December 6, 1986 apparently triggered another very strong supernova event which appears to lie on the same meridian as Betelgeuse. Since gravitational impulses are essentially instantaneous, the optical, i.e., electromagnetic effects, from a possible demise of Betelgeuse will not reach us for about 300 years, since Betelgeuse is about 300 light years away from us. However, if such an event did indeed occur, then we are in for one ‘helluva visual supernova’ at that time!
Another application for the electronic gravimeter is to provide a correction signal to ordinary scales based on Hooke’s Law mechanisms, i.e., springs. These errors are introduced by the earth gravity flux variations seen in Figure (5b) and appear on most such scale systems, including the most common digital-type bathroom scales. Many consumers complain of the weight variations they see on such scales --- they are real variations, but do not imply that one’s body mass is changing that rapidly! The author has demonstrated that such scale errors are correctable with gravimeters fed-back to the electrical readout of such units. However, these ‘errors’ should bring home to the amateur scientist the reality of these variations.
There are a great many other applications for gravimeters, especially the electronic versions, which will not be discussed here, but will come to the amateur researcher with increased understanding of the earth’s gravity as well as gravitation in general.
Conclusion:
This article is an attempt on the part of the author to introduce to the serious experimenter and the amateur scientist (and hopefully to the professional scientist as well) a new approach to the field of gravitation, especially the earth’s gravity field. Good experimetning to all!